Was wäre die ganze Technik ohne Zahnräder? Kein Getriebe würde es geben und damit auch keine Anpassung von Drehzahlen an den gewünschten Geschwindigkeitsbereich. Egal ob Maschinen oder Autos oder eben der Extruder unseres Druckers: Alle haben Zahnräder.
Ich wurde jetzt langsam neugierig darauf, wie man Zahnräder und deren Paarungen selbst berechnet, konstruiert und druckt. Der letzte Teil ist mir ja schon oft geglückt. Bei dem Einen oder Anderen meiner Leser verrichten von mir gedruckte Zahnräder ihren Dienst im Extruder. Ich will in zwei Beiträgen zunächst die Theorie und die notwendigen Berechnungen vorstellen und dann im zweiten Teil auf die Konstruktion in FreeCAD eingehen.
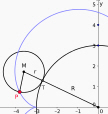
Die heute typischerweise industriell gefertigten Zahnräder haben Zähne, die auf einer Evolventenkonstruktion basieren. Geschichtlich gesehen ist das allerdings schon der zweite Schritt der mathematisch geometrischen Betrachtung von Zahnrädern. Angefangen hat es mit Epizykloiden. Um 1674, so vermutet man, kam der dänische Astronom Rømer beim Bau eines seiner Planetarien auf die Idee bei den Zähnen von Stirnzahnrädern eine von Epizykloiden abgeleiteten Form zu nutzen. Erst viele Jahre später lieferte Philippe de La Hire in seinem 1730 veröffentlichten Werk Traite des epicycloides die mathematische Untersuchung dazu nach. Vorher hatten alle Typen von Zahnrädern zumindest zwei große Nachteile: Bei der Übertragung der Drehbewegung kam keine kontinuierliche gleichmäßige Bewegung zustande. Noch viel schlimmer war aber der Umstand, dass durch das Fehlen einer gleichmäßigen Gleitreibung Zahnräder keine große Lebensdauer hatten. Eine Epizykloide entsteht, wenn man einen Kreis auf einem größeren Kreis abrollen lässt und dabei einen Punkt auf dem kleineren abrollenden Kreis verfolgt.
Schließlich perfektionierte Leonhard Euler um 1760 die Form, als er die Evolvente als Zahnform vorschlug. Die Evolvente wiederum erhält man gedanklich, wenn man ein Rad auf ein Blatt Papier legt. Dann wickelt man einen Faden einmal um das Rad. An einem Ende ist der Faden am Radumfang befestigt. Am anderen Ende des Fadens ist ein Stift befestigt. Wickelt man nun den Faden ab und lässt den Stift bei gestrafftem Faden über das Blatt Papier laufen, erhält man die Evolvente, die sogenannte Fadenkurve.
Heutige industriell gefertigte Stirnzahnräder haben üblicherweise diese Zahnform. Sie hat sich zum Standard entwickelt.
Für die ausführliche Geschichte möchte ich aber auf die Fachliteratur und auf die Wikipedia verweisen aus der auch das obige Bild entliehen ist.
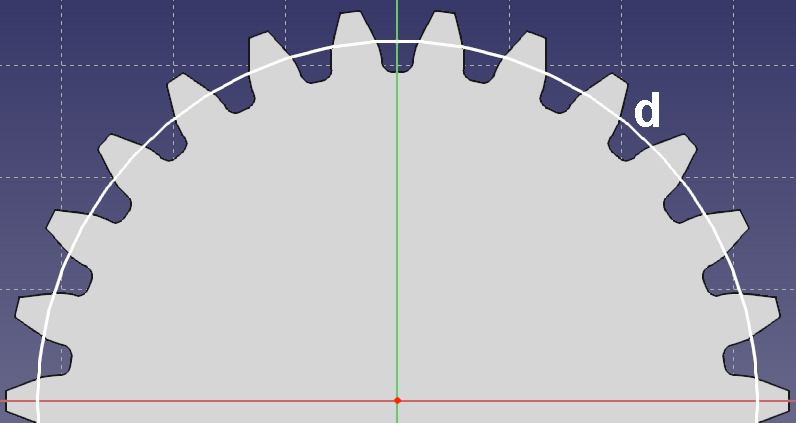
Die wohl wichtigsten Kennzahlen am einzelnen Zahnrad sind der Modul m und der Teilkreisdurchmesser d. Der Modul gibt letztlich die Größe der Zähne an. Der Teilkreisdurchmesser ist ein gedachter Kreis in etwa durch die Mitte der Zahnflanke. Zwei Zahnräder im direkten Eingriff haben einen gemeinsamen Teilkreisdurchmesser.
Daraus ergibt sich dann auch gleich die Erkenntnis, dass die Addition der beiden beteiligten Zahnkreisradien genau dem Achsabstand der beteiligten Zahnräder entspricht.
Achsabstand a = ( d1 + d2) / 2
Der Modul ergibt sich aus der Rechnung
Modul m = d / z
wobei z die Anzahl der Zähne darstellt. Mit etwas geometrischer Vorstellungskraft kann man jetzt leicht folgern, dass die Größe des Moduls auch die Größe der Zähne bestimmt.
Der Abstand von Zahnmitte zu Zahnmitte
p = m * Pi
was sich leicht über den Kreisumfang U = d * Pi ermitteln lässt.
Die letzte wichtige Größe gehört zu dem Umstand, warum man überhaupt ein Getriebe baut. Das Übersetzungsverhältnis von einem zum anderen Rad. Wir geben ihm den üblichen Buchstaben i.
Übersetzung i = d2 / d1
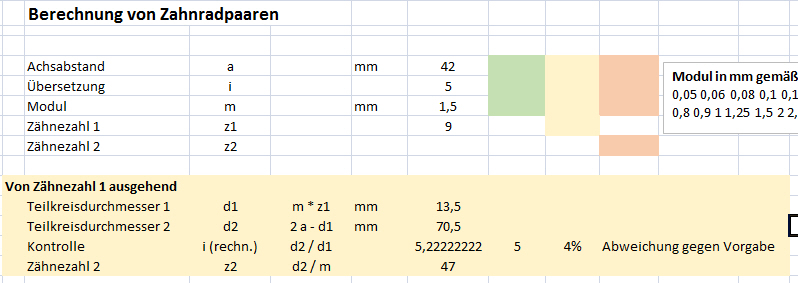
Ich habe ein kleines Excelblatt erstellt, mit dem man sich sehr leicht die gewünschten Werte errechnen kann:
Nebenbei sind nochmal sämtlich Formeln dargestellt und die die Modul-Vorzugsreihe nach DIN780 ist auch enthalten.
Ausgehend vom oberen Bereich startet man mit der Berechnung:
Der Achsabstand dürfte ja bekannt sein, – ebenso die gewünschte Zielübersetzung. Eine geschickte Wahl des Moduls ist ein wenig Erfahrungssache und sollte sich an der nebenstehenden Tabelle orientieren. Die Größe von Zahnrädern wie etwa beim Extruder berechnet man ganz gut mit einem Modul von 1,5mm.
Man kann jetzt die Zähnezahl des antreibenden Rades oder des abtreibenden Rades wählen. Die Paarung des Wade-Extruders ist übrigens 9 (Antrieb) und 47. Die Farben zeigen, in welchem der folgenden Blöcke gemäß der Eingaben das Ergebnis steht. Die Werte werden aber alle untereinander in Spalte G eingegeben, nicht in den Farbfeldern.
Mit den eingegebenen Daten liegen wir 4% neben dem Zielwert, – das ist nicht schlecht. Statt z1 kann natürlich auch z2 vorgegeben werden. Dann gibt es Ergebnisse im roten Feld.
Es geht aber noch einfacher. Mit den drei erstgenannten Eingaben a, i und m kann man auch eine automatisierte Berechnung durchführen. Und die wird im grünen Feld gezeigt. Etwas weiter unten auf dem Excelblatt sieht man die zugrundeliegende Tabelle, die jeweils neu errechnet wird. Danach werden die Werte der geringsten Abweichung für die Übersetzung ins grüne Feld kopiert.
Hellblau ist der Bereich für die Schrägverzahnung markiert. Üblicherweise ist Schrägverzahnungen oder Heringboneverzahnungen der Vorzug zu geben, da sie bedeutend laufruhiger sind und beim zweitgenannten sogar selbstzentrierend sind.
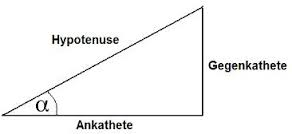
Ausgangsdaten sind hier der Verzahnungswinkel und die beidenTeilkreisdurchmesser. Die CAD-Software kann aber mit dem Winkel nichts anfangen und deshalb benötigen wir hier die Steigung. Das ist genau das Gleiche wie eine Gewindesteigung. Wieviele Millimeter steigt ein Gewindegang bei einer Umdrehung? Wickelt man den Gewindegang ab, kommt man zu einem rechtwinkligen Dreieck dessen Ankathete den Umfang des Teilkreises bildet und dessen Gegenkathete die Steigung beschreibt.
Über den Tangens kann diese Beziehung berechnet werden. Kleine Kontrolle hier: Die Steigung 2 ist ein Vielfaches der Steigung 1, es sei denn, die Durchmesser sind gleich und das Übersetzungsverhältnis deshalb auch gleich 1. Ansonsten ist der Faktor genau gleich dem Übersetzungsverhältnis.
Lasst Euch nicht von der Theorie erschlagen. Ich wollte hier nur mal die theoretische Herleitung zeigen. Ich habe mir die ganzen Informationen zu Zahnrädern selbst erst in den letzten Tagen heraus gesucht.
Der zweite Teil wird ein komplettes Beispiel inklusive Konstruktion in FreeCAD beinhalten.



Danke für die Ausführungen, hat mir sehr beim Verstehen geholfen, nun hab ich meine Zahnräder für den neuen Extruder selbst mit Freecad erschaffen können.
Hallo, vielen Dank für diesen Beitrag! Das ist eine sehr interessante Idee, die Zahnräder und deren Paarungen selbst zu berechnen. Würde ich gerne auch selbst probieren. Ich kann mir aber sehr gut vorstellen, dass die Auswahl des richtigen Materials und des geeigneten Fertigungsverfahrens nicht so einfach zu entscheiden wären.
Vielen Dank für den interessanten Beitrag zum Thema Berechnung von Zahnrädern! Im Rechnen war ich leider noch nie ganz fit, doch die Berechnungen hierfür traue ich mir sogar zu. Noch mehr interessiert mich die Konstruktion von Zahnrädern. Deshalb bin ich sehr froh, dass ich jemanden kenne, der mir ermöglichen kann, mal intern in den Konstruktionsprozess hineinzusehen.